摘要：
快速排序是一种常用的排序算法，它的核心思想是通过不断地将数组分割为较小和较大的子数组，然后递归地排序子数组。本文将详细介绍如何实现分割数快速排序算法，帮助读者更好地掌握这一算法。... 快速排序是一种常用的排序算法，它的核心思想是通过不断地将数组分割为较小和较大的子数组，然后递归地排序子数组。本文将详细介绍如何实现分割数快速排序算法，帮助读者更好地掌握这一算法。
1.理解快速排序算法的基本原理
通过对数组进行分割和递归操作，快速排序能够将一个无序的数组转化为有序的数组。
2.实现分割函数
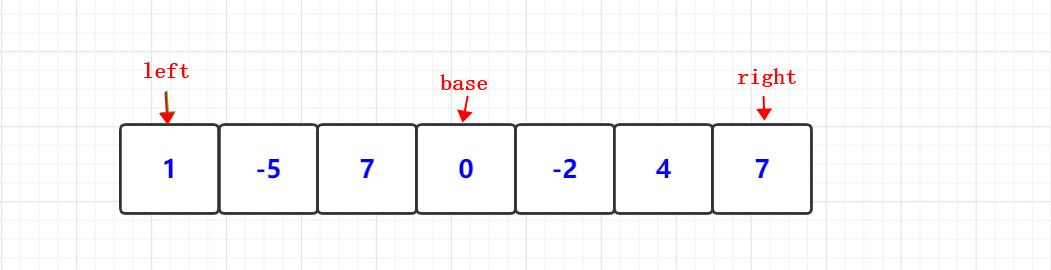
分割函数是快速排序算法中最重要的一步，它将数组根据一个基准值分成较小和较大两部分，并返回基准值的索引。
3.选择合适的基准值
选择合适的基准值可以提高快速排序的效率，常用的方法有随机选择、选择首、中、尾元素的中间值等。
4.调用分割函数进行数组分割
利用编写好的分割函数，将整个数组进行分割，得到较小和较大的两个子数组。
5.对子数组进行递归排序
对较小和较大的两个子数组分别进行递归排序，直到子数组长度为1时停止递归。
6.组合子数组得到排序好的数组
通过递归排序得到的有序子数组，将它们组合起来，得到完全有序的数组。
7.处理特殊情况
考虑到数组中可能存在相同元素的情况，我们需要在分割函数中进行特殊处理，确保算法的正确性。
8.分析快速排序的时间复杂度
通过分析每一步的时间复杂度，我们可以得出快速排序的平均时间复杂度为O(nlogn)。
9.优化快速排序算法
针对快速排序可能出现的最坏情况，我们可以通过随机选择基准值、三数取中等方法进行优化。
10.快速排序与其他排序算法的比较
对比快速排序与其他经典排序算法，如冒泡排序、插入排序等，分析其优势和不足之处。
11.快速排序在实际应用中的应用场景
介绍快速排序在实际应用中的一些常见场景，如查找中位数、寻找前k个最大或最小元素等。
12.使用示例演示快速排序的过程
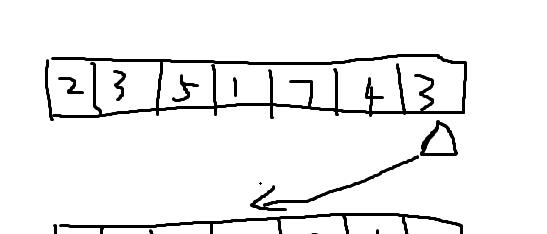
通过一个具体的示例演示快速排序的具体过程，帮助读者更好地理解和掌握算法。
13.快速排序的稳定性讨论
快速排序是一种不稳定的排序算法，我们将对其稳定性进行讨论，并举例说明。
14.快速排序的空间复杂度分析
通过分析快速排序算法的递归调用栈以及额外空间的使用情况，得出其空间复杂度为O(logn)。
15.
快速排序算法的核心思想、步骤和优化方法，并对其在实际应用中的优缺点进行概括。
通过阅读本文，读者能够全面了解快速排序算法的实现原理、优化方法以及在实际应用中的应用场景，从而更好地掌握这一重要的排序算法。
