摘要：
快速排序是一种常用的排序算法，它的核心思想是通过将数组分成两个子数组并对这两个子数组进行递归排序来实现整个数组的有序。其中，选择合适的分割数对算法的效率有重要影响。本文将围绕分割数... 快速排序是一种常用的排序算法，它的核心思想是通过将数组分成两个子数组并对这两个子数组进行递归排序来实现整个数组的有序。其中，选择合适的分割数对算法的效率有重要影响。本文将围绕分割数快速排序展开讨论，介绍如何优化算法，实现快速排序以及分割数策略，并对其时间复杂度进行分析。
一什么是分割数快速排序
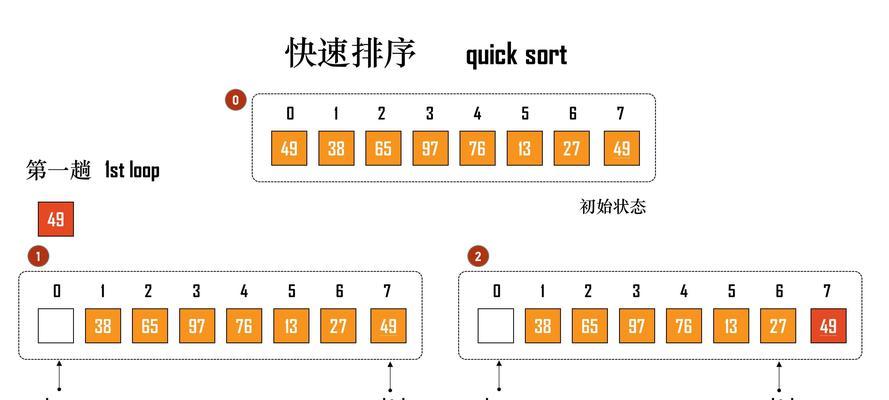
分割数快速排序是一种基于快速排序算法的改进方法，它通过选择合适的分割数来提高排序的效率。在传统的快速排序算法中，通常选择数组的第一个元素或者随机选择一个元素作为分割数，但这种选择可能导致不均衡的划分，影响排序的效率。而分割数快速排序通过采用更优的选择策略，能够更好地将数组分割成两个近似相等的子数组。
二如何实现快速排序算法
实现快速排序算法需要进行递归地划分子数组和对子数组进行排序。具体步骤如下：选择一个分割数；将数组按照分割数划分成两个子数组，比分割数小的放在左侧，大的放在右侧；接着，递归地对左右两个子数组进行快速排序；将排序后的左右子数组合并成一个有序数组。
三如何选择合适的分割数
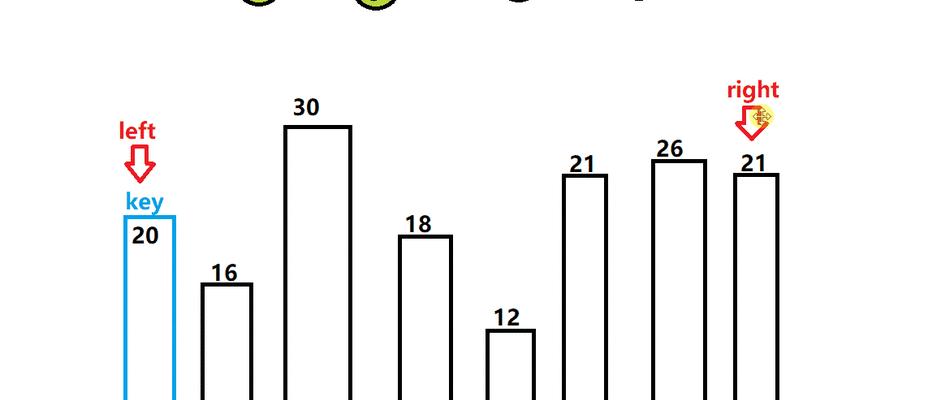
选择合适的分割数是分割数快速排序的关键。常见的选择策略有三种：使用第一个元素作为分割数、随机选择一个元素作为分割数以及使用中值作为分割数。其中，使用中值作为分割数的方法相对较为优化，可以尽可能地避免不均衡的划分，提高排序效率。
四时间复杂度分析
分割数快速排序的时间复杂度主要取决于划分子数组的平衡性。在最坏情况下，如果每次划分都只能将数组划分成1:9的比例，时间复杂度将退化为O(n^2)。而在平均情况下，如果每次划分都能得到近似相等的子数组，时间复杂度将为O(nlogn)，与传统快速排序相同。
五优化算法：随机选择分割数
为了避免最坏情况下的时间复杂度退化，可以采用随机选择分割数的策略。随机选择一个元素作为分割数可以在一定程度上降低不均衡划分的概率，提高排序效率。
六优化算法：三数取中作为分割数
另一种优化策略是使用中值作为分割数。具体方法是从数组的首、中、尾三个元素中选择中间大小的元素作为分割数，这样可以减少不均衡划分的可能性，进一步提高排序效率。
七优化算法：插入排序优化小规模子数组
对于小规模的子数组，快速排序可能会退化为较慢的算法。为了解决这个问题，可以采用插入排序算法对小规模子数组进行排序，从而提高整体的排序效率。
八优化算法：使用三向切分
三向切分是另一种优化算法，适用于存在大量重复元素的情况。它通过将数组分割成小于、等于和大于分割数的三个部分，减少了重复元素的比较和交换次数，提高了排序效率。
九优化算法：尾递归优化
尾递归是一种优化技术，可以减少函数调用的开销。在快速排序算法中，可以尝试使用尾递归来优化递归排序的过程，降低空间和时间复杂度。
十分割数快速排序的稳定性问题
分割数快速排序是一种不稳定的排序算法，因为在交换元素的过程中，相等元素的相对顺序可能会发生改变。如果需要保持相等元素的相对顺序不变，可以考虑使用稳定的排序算法。
十一应用场景与实践意义
分割数快速排序适用于大规模数据的排序，尤其是当数据中存在大量重复元素时。通过选择合适的分割数和采用优化算法，可以在实际应用中提高排序效率，节省时间和计算资源。
十二分割数快速排序的局限性
分割数快速排序的主要局限性在于最坏情况下时间复杂度的退化和不稳定性。在处理特定类型数据时，可能会出现效率不高的情况。此外，递归调用可能导致栈溢出的问题。
十三与其他排序算法的比较
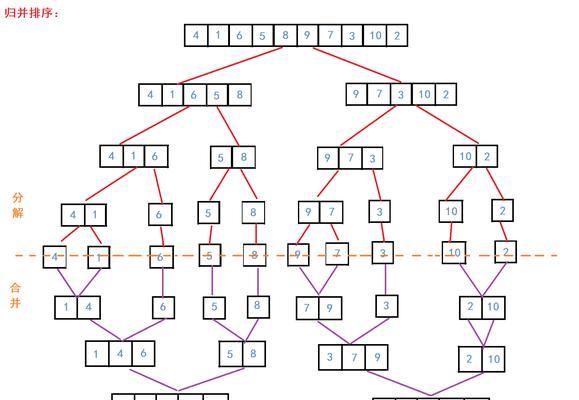
与其他常见的排序算法相比，分割数快速排序具有较好的平均时间复杂度和空间效率。然而，在某些特殊情况下，其他排序算法如归并排序和堆排序可能更适合。
十四分割数快速排序的优化方法
分割数快速排序可以通过选择合适的分割数、优化划分子数组、使用尾递归等方法来提高排序效率。然而，它也存在不稳定性和时间复杂度退化的问题，适用范围有限。
十五展望分割数快速排序的未来发展
随着计算机技术的不断进步和算法研究的深入，分割数快速排序仍有进一步优化和改进的空间。未来的发展方向可能包括更精确的分割数选择策略、更高效的划分子数组算法等，以进一步提高排序效率。
